AVL Tree

The AVL Tree came from its inventor's name Adelson Velskii Landis. It is self-balancing binary tree also known as the Height Balanced Binary Tree.

In the AVL tree, the height of two sub trees of the node may differ by at most one. It structure is the same as the binary search tree, but with little difference. The advantages of AVL tree are that it takes O(log n) time to perform searches, insert, delete operations in the average case as well as the worst case. It means, the operations like insertion and deletion have low time complexity.

Balance Factor

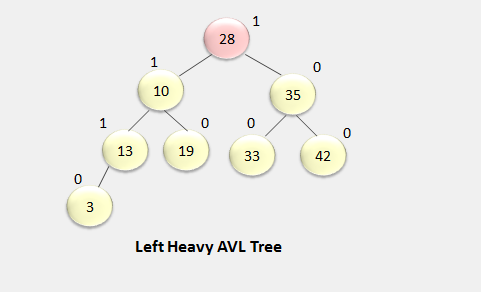
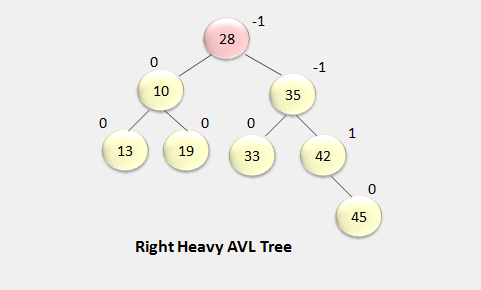
The balance factor is calculated by subtracting the height of its right sub-tree from the height of the left sub-tree. So the balance factor of -1, 0, 1 is considered to be a height-balanced tree. A node with anything other than this value is considered to be unbalanced and needs to be rebalancing.

A balanced tree has the following properties.

• If the left sub tree has the longest path than the right subtree, then it is left heavy AVL tree.
• If the right sub tree has the longest path than the left subtree, then it is right heavy AVL tree.
• If the left and right sub tree has an equal path, then it is a balanced AVL tree.