Depth First Search

The Depth First Search is also an algorithm for a graph traversal. It begins at the root node and explores in depth along each branch. It is like a pre-order traversal of the tree.

DFS is a better traversal technique than BFS. It maintains a few pointers at each level.

The DFS is basically used to solve problems like - Hopcroft-Karp, traveling-salesman problem, topological sorting etc.

Algorithm for depth-first-search

These are the steps for the Depth-First-Search algorithm -

Initially, take an empty stack, pick a node and PUSH all its adjacent nodes into a stack.
POP(removed) a node from the stack, marked it as visited and PUSH all its neighbour nodes into a stack.
Repeat the above process till the stack becomes empty.

Step 1: SET STATUS = 1 (ready state) for each node in G
Step 2: Push the starting node A on the stack and set
its STATUS = 2 (waiting state)
Step 3: Repeat Steps 4 and 5 until STACK is empty
Step 4: Pop the top node N. Process it and set its
STATUS = 3 (processed state)
Step 5: Push on the stack all the neighbours of N that
are in the ready state (whose STATUS = 1) and
set their STATUS = 2 (waiting state)
[END OF LOOP]
Step 6: EXIT

Example of Depth First Search

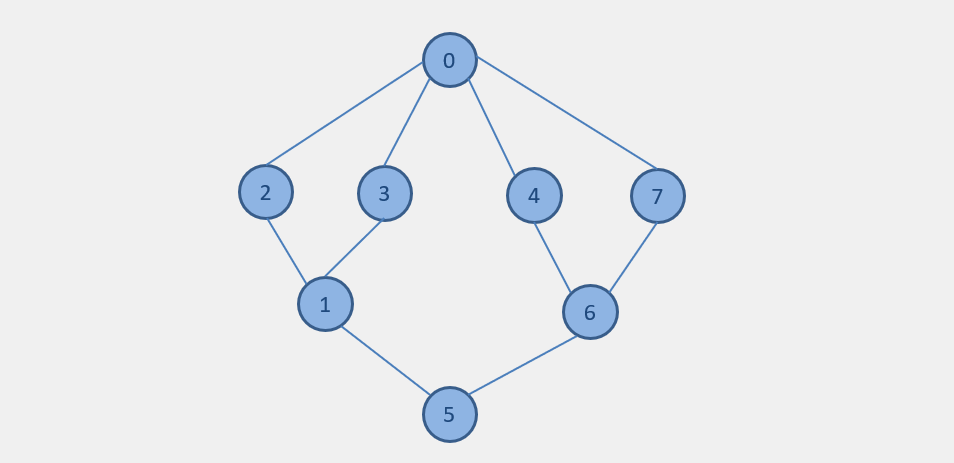
The Depth First Traversal of the above graph is -

DFS : 1 3 2 8 7 4 5

Complexity of Depth First Search

Time Complexity of DFS in Tree Traversal

If V is the number of nodes in a tree, the time complexity to be traversed is O(V).

Time Complexity of DFS in Graph Traversal

If V is the number of vertexes and E is the number of edges in a graph, the time complexity to be traversed is O(V + E).

Depth First Search Program in C

#include<stdio.h>
#include<stdlib.h>
 
typedef struct node
{
    struct node *next;
    int vertex;
}node;
 
node *Graph[50];   
int visited[50];
int n;
void create_graph(); 
void insert_vertex(int,int);  
void DFS(int);
 
void main()
{
    int i;
    create_graph();
   
	for(i=0;ivertex;
       
	   if(!visited[i])
            DFS(i);
        p=p->next;
    }
}
 
void create_graph()
{
    int i,vi,vj,no_of_edges;
    printf("Enter number of vertices:");   
	scanf("%d",&n);
   
	for(i=0;ivertex=vj;
    q->next=NULL;
 
    if(Graph[vi]==NULL)
        Graph[vi]=q;
    else
    {
        p=Graph[vi];
       
		while(p->next!=NULL)
        	p=p->next;
			p->next=q;
    }
}

Output of the above program

Enter number of vertices:8
Enter number of edges:10
Enter an edge(u,v):0 2
Enter an edge(u,v):0 3
Enter an edge(u,v):0 4
Enter an edge(u,v):0 7
Enter an edge(u,v):2 1
Enter an edge(u,v):3 1
Enter an edge(u,v):4 6
Enter an edge(u,v):7 6
Enter an edge(u,v):1 5
Enter an edge(u,v):1 6

0
2
1
5
6
3
4
7