Breadth First Search
Graph Traversal means visiting each node exactly once. There are two methods of traversing the graph-
- Breadth First Search (BFS)
- Depth First Search (DFS)
Breadth First Search
The Breadth First Search is an algorithm for a graph or a tree traversal. It begins at the root node and explores all the neighbouring nodes in breadth(full-graph width) before going in deeper. A queue and a graph or a tree are used as a data structure in a breadth first algorithm.
In this, the traversal of elements of a graph or tree goes through level-by-level(left to right). It makes sure that every node is visited at least once. In each iteration, a vertex is removed from the queue and the adjacent vertices which are not visited are added in a queue. This algorithm terminates when the queue becomes empty.
The BFS is basically used to solve problems like - mapping routes, analyzing networks, puzzle game, scheduling, web crawlers etc.
The BFS is less space efficient than depth-first-search.
Algorithm for breath-first-search
These are the steps for the Breadth-First-Search algorithm -
- Initially, take an empty queue, pick a node and enqueue all its adjacent nodes into a queue.
- Dequeue(removed) a node from the queue, marked it as visited and enqueue all its neighbour nodes into a queue.
- Repeat the above process till the queue becomes empty.
Step 1: SET STATUS = 1 (ready state)
for each node in G
Step 2: Enqueue the starting node A to queue and mark it visisted
and set its STATUS = 2
(waiting state)
Step 3: Repeat Steps 4 and 5 until
QUEUE is empty
Step 4: Dequeue a node N. Process it
and set its STATUS = 3
(processed state).
Step 5: Enqueue all the adjacents of
N that are in the ready state and mark them visisted
(whose STATUS = 1) and set
their STATUS = 2
(waiting state)
[END OF LOOP]
Step 6: EXITComplexity of Breadth First Search
Time Complexity of BFS in Tree Traversal
If V is the number of nodes in a tree, the time complexity to be traversed is O(V).
Time Complexity of BFS in Graph Traversal
If V is the number of vertexes and E is the number of edges in a graph, the time complexity to be traversed is O(V + E).
Example of Breadth First Search
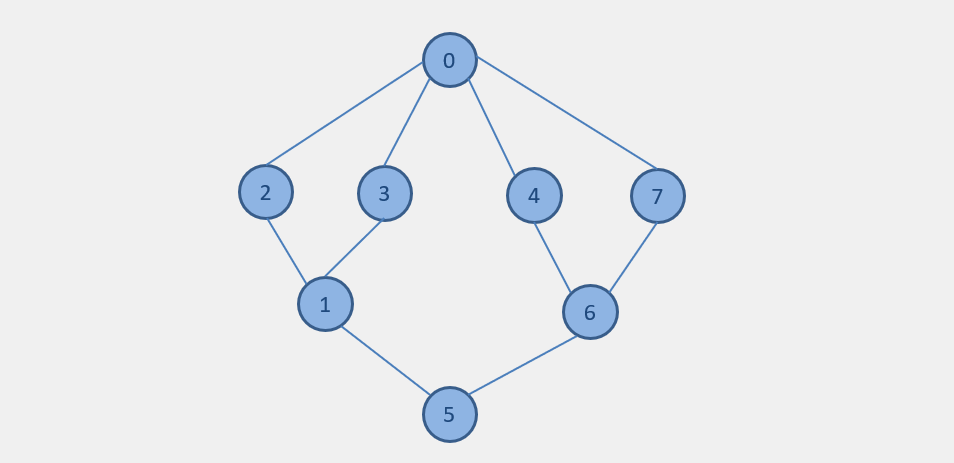
BFS : 0 2 3 4 7 1 6 5
Bredth First Search Program in C
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
#define initial 1
#define waiting 2
#define visited 3
int n;
int adj[MAX][MAX];
int state[MAX];
void generate_graph();
void bfs_traversal();
void BFS(int v);
int queue[MAX], front = -1,rear = -1;
void enqueue(int vertex);
int dequeue();
int check_emptyqueue();
int main()
{
generate_graph();
bfs_traversal();
return 0;
}
void bfs_traversal()
{
int v;
for(v=0; v rear)
return 1;
else
return 0;
}
int dequeue()
{
int delete_item;
if(front == -1 || front > rear)
{
printf("Queue Underflow\n");
exit(1);
}
delete_item = queue[front];
front = front+1;
return delete_item;
}
void generate_graph()
{
int count,max_edge,origin,destin;
printf("Enter number of vertices : ");
scanf("%d",&n);
max_edge = n*(n-1);
for(count=1; count<=max_edge; count++)
{
printf("Enter edge %d( -1 -1 to quit ) : ",count);
scanf("%d %d",&origin,&destin);
if((origin == -1) && (destin == -1))
break;
if(origin>=n || destin>=n || origin<0 || destin<0)
{
printf("Invalid edge!\n");
count--;
}
else
{
adj[origin][destin] = 1;
}
}
} Output of the above program:
Enter number of vertices : 8
Enter edge 1( -1 -1 to quit ) : 0
2
Enter edge 2( -1 -1 to quit ) : 0
3
Enter edge 3( -1 -1 to quit ) : 0
4
Enter edge 4( -1 -1 to quit ) : 0
7
Enter edge 5( -1 -1 to quit ) : 2
1
Enter edge 6( -1 -1 to quit ) : 3
1
Enter edge 7( -1 -1 to quit ) : 4
6
Enter edge 8( -1 -1 to quit ) : 7
6
Enter edge 9( -1 -1 to quit ) : 1
5
Enter edge 10( -1 -1 to quit ) : 6
5
Enter edge 11( -1 -1 to quit ) : -1-1
Enter Start Vertex for BFS:
0
0 2 3 4 7 1 6 5














