Graph Introduction

A Graph is a non linear data structure. It is often viewed as a generalization of the tree structure. It contains two main components vertices (nodes) and edges. Two nodes are connected via an edge. The graph is used to represent many computer applications, like - a computer network, in which nodes are network workstations and the edges are the network connections.

Formal Definition of Graph

A graph G is defined as an ordered set (V, E), where V(G) represents the set of nodes or vertices and E(G) represents the edges that connect these nodes.

Types of Graph

There are two types of Graphs -

Directed Graph

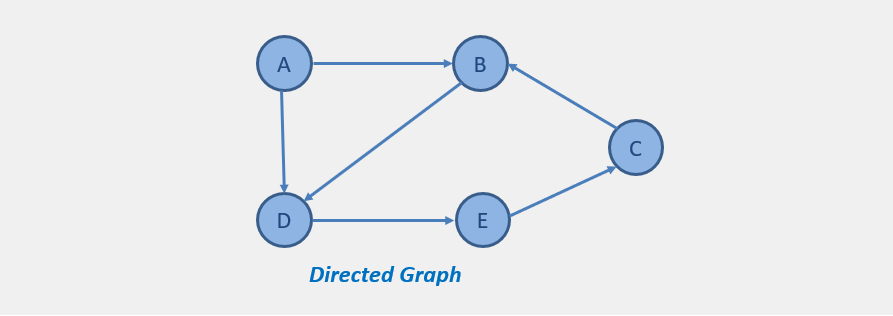
In a directed graph, there is a path between nodes. So, edges form an ordered pair. Suppose, there are two nodes A and B and there is an edge from A to B. Then the only possible path from A to B, but not from B to A.

A directed graph G is a graph in which an edge is given as an ordered pair (u,v) of nodes in G. So for the edge (u,v) -

• The edge starts at u and terminates at v.
• u is the initial point and v is the destination point.
• both nodes u and v are adjacent to each other.

Undirected Graph

In an undirected graph, there is no any directed edges between nodes. Suppose, there is an edge between node A to B, then we can easily traverse from A to B and from B to A.

Graph Terminology

These are the graph terminologies -

Adjacent Nodes - The edge E that connects nodes u and v, so the nodes u and v are adjacent to each other.

Degree of a node - The degree of a node is defined as the total number of edges connecting to the node.

Regular graph - If each vertex of a graph has the same number of neighbours, i.e., every node has the same degree, that is called regular graph.

Cycle - A path has the same first and last vertices are called cycle.

Connected Graph - A graph is said to be connected, for any two vertices (u,v) there is a path from u to v.

Complete Graph - A graph is said to be complete, if all its nodes are fully connected.

Weighted Graph - A graph is said to be weighted or labelled, if every edge in a graph is assigned some data. If e denotes the edge of a graph, then w(e) denotes the weight of a graph.

Multiple Edges - Distinct edges which connect the same end-points are called multiple edges.

Loop - An edge with identical end points is called a loop, i.e, e(u,u).

Multi-graph - A graph with multiple edges or loops is called a multi-graph.

Size of a graph - The total number of edges in a graph is the size of a graph.