Heap Sort

In Heap Sort, we are using Binary Search Tree for sorting. In this, all elements are inserted into tree. Heap sort requires more space than other sorting methods. It is stable sort and requires constant space for sorting.

Heap sort basically works in two phases.

Suppose an array A has n elements, it sorts the array in two phases.

First build a heap from elements of the array.
In the second phase, it repeatedly deletes the root element from the heap that built in the first phase and place the element in the last empty location of the array.

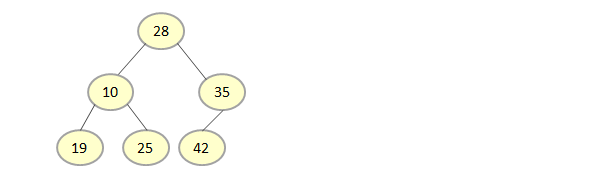
Arrange the elements to make a binary search tree.

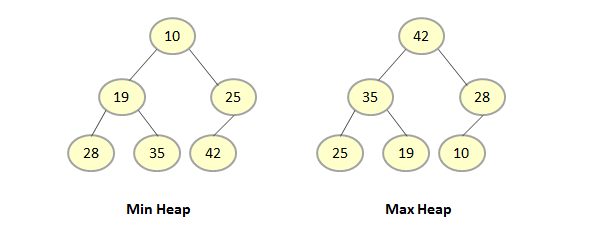
The heap tree can be of two types - Max Tree and Min Tree.

Max Tree - The root node has highest key value, then the child node elements.

Min Tree - The root node has lowest key value, then the child node elements.

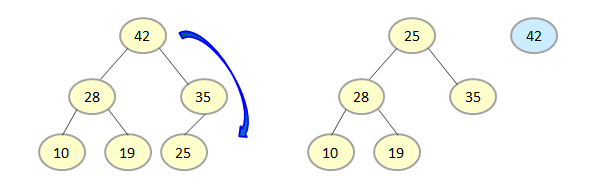
In this, the root element is compared with right child element, 42 > 25, so delete the root element and place in the last empty location of the array.

Again, compare the root element with the right child node and as 35 > 25, so first swap 35 and 25 element position and delete 35 from the root and store in the left of the array.

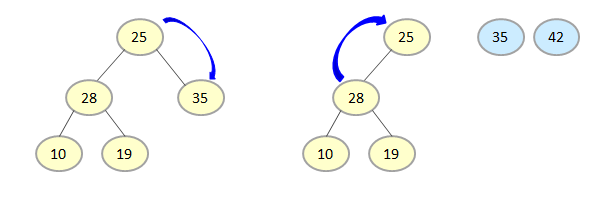
A repeat of the same process with the left elements, until all elements are deleted.

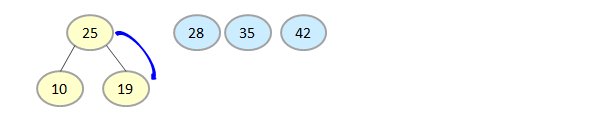
At last, we get two elements and do the same process remove the highest root element first.

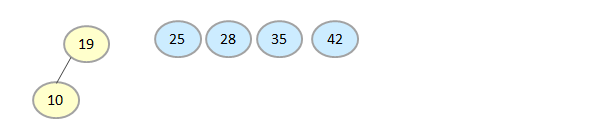
At last, we get the array fully with all elements in sorted order.

Complexity of Heap sort

Suppose n is the number of element in an array.

Best Case Time Complexity - O(n*log n)
Worst Case Time Complexity - O(n*log n)
Average Time Complexity - O(n*log n)

Heap Sort Program in C

#include<stdio.h>
#include<conio.h>


void heap_sort();

void heap_swap(int, int);
int array[50], t, a;

int main() {
  int i,size;

  printf("Enter the number of elements: ");
  scanf("%d", &size); 
  printf("Enter %d numbers : ",size);
  for (i = 0; i < size; i++)
    scanf("%d", &array[i]);

  printf("\nList of Sorting  :");
  for (i = 0; i < size; i++) {
    printf("\t%d", array[i]);
  }

  heap_sort(size);

  printf("\n\nSorted Data :");
  for (i = 0; i < size; i++) {
    printf("\t%d", array[i]);
  }

  getch();

}

void heap_sort(size) {
  	
  for (int i = size / 2 - 1; i >= 0; i--)
    heap_swap(size, i);

  for (int i = size - 1; i >= 0; i--) {
    // swapping values 
    t = array[0];
    array[0] = array[i];
    array[i] = t;
    heap_swap(i, 0);

    printf("\nHeap Sort Iteration %d : ", i);
    for (a = 0; a < size; a++) {
      printf("\t%d", array[a]);
    }
  }
}

void heap_swap(int n, int i) {
  int large = i, left = 2 * i + 1, right = 2 * i + 2;

  // swap left child
  if (left < n && array[left] > array[large])
    large = left;

  // swap right child
  if (right < n && array[right] > array[large])
    large = right;


  if (large != i) {
    // swapping values 
    t = array[i];
    array[i] = array[large];
    array[large] = t;
    heap_swap(n, large);
  }
}

Output of the above program:

Enter the number of elements: 10
Enter 10 numbers : 2
33
54
34
60
12
54
23
77
98

List of Sorting  :	2	33	54	34	60	12	54	23	77	98
Heap Sort Iteration 9 : 	77	60	54	34	33	12	54	23	2	98
Heap Sort Iteration 8 : 	60	34	54	23	33	12	54	2	77	98
Heap Sort Iteration 7 : 	54	34	54	23	33	12	2	60	77	98
Heap Sort Iteration 6 : 	54	34	12	23	33	2	54	60	77	98
Heap Sort Iteration 5 : 	34	33	12	23	2	54	54	60	77	98
Heap Sort Iteration 4 : 	33	23	12	2	34	54	54	60	77	98
Heap Sort Iteration 3 : 	23	2	12	33	34	54	54	60	77	98
Heap Sort Iteration 2 : 	12	2	23	33	34	54	54	60	77	98
Heap Sort Iteration 1 : 	2	12	23	33	34	54	54	60	77	98
Heap Sort Iteration 0 : 	2	12	23	33	34	54	54	60	77	98

Sorted Data :	2	12	23	33	34	54	54	60	77	98